Aquí en esta entrada vamos a prepararnos para las Olimpiadas de Matemáticas de Bachillerato. Os propongo distintos problemas que han ido saliendo en otras ediciones y otros para que vayamos entrenando.
- Calcula el valor de la expresión: [(secx+cosecx)²+(tgx+cotgx)²].sen2x
- Determinar x, y, z en el número 33xy49z para que sea múltiplo de 693.
- Demuestra que la suma de cubos de 3 números naturales consecutivos es un número múltiplo de 9.
- Hallar todas las funciones reales continuas
que cumplen, para todo x real positivo, la condición 
- Hay 9 hermanos y nacieron todos con intervalos de 3 años. El menor es 3 veces más joven que el mayor. ¿Cuánto suman sus edades?.
- El número de 4 cifras aabb es un cuadrado perfecto. ¿Qué número es?.
- Suponga que se quiere expandir la expresión
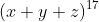. ¿Cuál es el coeficiente del término 
?. - Verificar que la siguiente igualdad es cierta 1 + 3 + 5 +… + (2n-1) = n²
- Calcular la suma de los cuadrados de los 100 primeros términos de una progresión aritmética, sabiendo que la suma de ellos vale -1 y que la suma de los términos de lugar par vale 1.
- Encuentre el resultado de la siguiente suma:
- Encontrar todos los números enteros positivos a, b, c ≥1 que satisfacen:
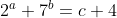
- Las longitudes de los lados de un triángulo están en progresión geométrica de razón r. Halla los valores de r para que el triángulo sea, respectivamente, acutángulo, rectángulo u obtusángulo.
